*current address:
Ohio Aerospace Institute
NASA Lewis Research Center, 302-1
21000 Brookpark Rd.,
Cleveland, OH 44135
Abstract
A proposal for a laser-pushed light sail as a means of propelling an interstellar probe is analyzed. High mass ratios are avoided by using a stationary energy source. The large lens required and high lens/target distance results in an extremely high optical magnification, which presents alignment and positioning difficulties. Some advantage can be gained by using a lightsail reflective in a shorter wavelength regime. Another technique for reducing the problem would be to use many intermediate lenses spaced between the probe and the source. Pointing, positioning, and deployment problems would, however, be great. Various sail materials were considered in view of materials parameters, reflectivities, and melting point. Quarter wavelength dielectric films have significant advantages over metals as sail materials. The best figure of merit was for a SiC film, with a figure of merit of 60 km2/kg, allowing a theoretical acceleration of 0.4 gravities per mW/cm2 of laser power. High accelerations are achievable with available laboratory lasers to test potential technologies.
This work was done while the author was a NASA/NRC resident research associate at NASA Lewis Research Center.
Copyright 1989 by Geoffrey A. Landis; all rights reserved. Published by the International Astronautical Federation and the American Institute of Aeronautics and Astronautics, Inc., with permission
Nomenclature
a = effective laser aperture
c = speed of light
d = inter-lens spacing
F = force
j = intermediate lens number
m
lens = mass of the lensm
sail = mass of the sailn = index of refraction.
N = number of intermediate lenses used
P = power in watts
R = reflectance
r = lens radius
s = distance.
T = temperature in degrees Kelvin
Tm = melt temperature
t = thickness of a quarter-wavelength film
D
y = error in beam position at sailD
x = error in position at sourcee
= thermal emissivityl =
laser wavelengthr =
density.Introduction
An interstellar probe presents an extremely challenging problem to space propulsion technology. Since the distances to the nearest stars are four light years and more, probe velocities must be a significant fraction of the speed of light for travel times to be less than many decades. For conventional propulsion systems, the required mass ratios are prohibitive. This has led to interest in beamed propulsion systems, in which the propulsion source is fixed, and only the probe accelerated. One such system is the laser-propelled lightsail, first proposed by Forward [1] in 1962 and by Marx [2] in 1966, in which a very large, light-weight reflective sail is propelled using the energy from a fixed laser.
An article on round-trip interstellar travel using a laser-propelled lightsail [3] has drawn significant attention. It is worthwhile to comments on some of the optics and materials issues raised.
In a laser (or microwave) propelled sail, a fixed energy source beams power to a reflective sail. Thrust is produced by the reflection of the electromagnetic beam from the sail. For a non-relativistic sail with perfect reflection, the force imparted is:
F = 2P/c. (1)
In practical units, this is a force of 6.7 newtons per gigawatt. This is an extrordinarily low energy efficiency; e.g., one gigawatt is the output of a typical small nuclear power plant. The advantage comes from the fact that no fuel is carried on board, and thus the specific impulse is infinite. The sail is constructed out of a metallic film only a few tens of nanometers thick, and thus is very light.
A related concept is that of a microwave-pushed sail [4,5], where the propulsion beam is a microwave beam and the sail is a thin metal mesh. In optics terms, this concept is identical to that of the laser-pushed sail, but the sail and lens are mesh, rather than solid films, and the characteristic size of the system must be scaled up due to the longer wavelengths of microwaves compared to light.
A lens is required to keep the beam spread due to diffraction at the aperture low. The diffraction-limit to beam spread is
Dy > 2.44 l s /a (2)
where
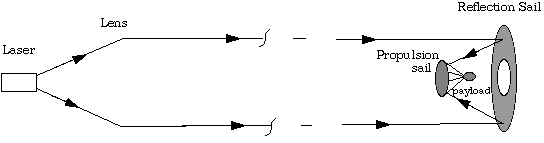
l is the laser wavelength, a the effective laser aperture and s the distance. (The laser spot actually has an exponential tail outside this distance, but 84% of the light falls within the limit listed). To minimize the beam spread, a large lens is used. The effective aperture is then equal to the lens radius rather than the physical size of the laser. Forward proposes that sufficiently large lenses (thousands of kilometers) can be made using the "paralens" concept; alternating rings of thin material with refractive index n alternating with empty space to form a very large fresnel zone plate. Thickness of the rings is a multiple of a half wavelength, resulting in interference producing nearly zero surface reflection.A significant portion of the problem is decelerating at the target. In the basic concept proposed by Forward [3], a three part lightsail is used. At the target star, the sail is separated into two parts. One part of the sail reflects the light backwards onto the second part, which carries the vehicle, to decelerate it to rendezvous. Fig. 1 shows this in schematic form. For the return trip, the sail separates once again, to reflect the remote laser onto the ship.
A disadvantage of the round-trip propulsion system is that it is poorly suited for a small probe mission, since the lens and sail sizes must be large due to the beam spread over interstellar distances. This is not a problem for a fly-by mission, however, and it is possible that a demonstration probe could be considerably smaller than the one ton mission proposed.
The stopping efficiency of the sail is low. The mass ratio (decelerator sail to reflector reflector sail) is one tenth, and the energy efficiency of the reflection, due to doppler shift and losses in the reflector sail, is about 1/3. Never the less, this mass ratio is better than can be achieved by conventional means, or even by a fusion rocket, to decelerate from a maximum velocity of half the speed of light.
Forward compares this with decelerating by electrically charging the probe to turn using the Lorentz force in the interstellar magnetic field [6,7], reversing the sail velocity so that the laser can decelerate it. He concludes that there is sufficient doubt about the strength of the interstellar magnetic field that we do not know if this is possible.
Andrews and Zubrin [8], as a section of their paper on braking interstellar ships using drag from the interstellar medium or the solar wind, discuss several difficulties relating to the difficulty of maintaining a focused beam. They note that for the two-stage lightsail, the mirror must maintain surface quality to an unlikely tolerance as it decelerates the second stage (this was also noted by Forward [3] as a major unstudied problem in the conclusion of his paper). They also discuss the fact that the laser dispersion due to beam quality, jitter, etc. must be considerably better than beam qualities of existing state of the art beams. Much of the difficulties in beam quality that they discuss could be ameliorated by using a single master oscillator for all of the laser amplifiers in the source. Finally, they note that the required pointing accuracy is four orders of magnitude better than the current state of the art (Hubble space telescope). They discuss use of a laser for initial acceleration and a combination of a magnetic sail and fusion rocket for deceleration, concluding that a 10 ly journey could be made in slightly over a hundred years.
Optics Considerations
Table 1 summarizes the three missions considered by Forward. The first mission is for a flyby with no deceleration at the target star. The vehicle is a 4 kilometer sail accelerated for to 0.17 ly from the solar system and then coasts at constant velocity to the target star. A 1000 km lens assumed to be 15 AU (2 1012 m) from the laser and focused onto a spot 0.17 light-years (1.6 1015 m) away.
The optical problem for the first (flyby) mission is shown in fig. 2. The optical magnification of the lens (= the ratio of image to object distance) is thus 715 X, and the error
D y in beam position at sail equals 715 times the error Dx in source position. The light will miss the sail if it is misdirected by more than half the sail diameter, or 2 km; the performance will decrease if the light is misdirected by even a fraction of this. This implies several things [9]:(The total beam spread is actually the RMS sum of contributions from each of the individual errors, diffraction, lens positioning error, laser positioning error, and the beam quality.)
It is hard to believe that a 1000 km lens could be positioned to within 3 meters.
The second mission proposed by Forward would be a rendezvous using a 100 km sail. For this mission the laser must be focused at a distance of 4 ly. The larger distance nullifies the larger sail, so that the positioning accuracy is still 5 meters. For the manned mission to epsilon Eridani, 10.8 ly away, the most stringent requirement is to hit the 320 km reflector sail, which must focus onto the 100 km return sail. (The difficulties involved in this focussing are enormous, although not discussed here.) The optical magnification of the lens system is 50,000, and to hit a 320 km sail, the lens must be again be positioned to within 3 meters.
The lens positioning problem is related to the pointing accuracy of the lens. For an interstellar journey, the lens must be pointed to an accuracy equal to the sail diameter at a distance of the interstellar distance, requiring a pointing accuracy of (sail radius)/(star distance). This is an extremely stringent pointing requirement regardless of the tricks used to position the lens. The pointing accuracy about one picoradian (0.2 micro arc-seconds). While extremely slowly changing errors in the position may be compensated by adjusting the probe position to follow the varying beam, this will not work for faster jitter in the beam.
It is clear that interstellar lasersailing must use larger sails, and that the wavelength used must be as short as possible to reduce beam spread.
From eqn 2 we see that it is desirable to decrease the laser wavelength as much as possible, even if the penalty is some drop in efficiency. Free-electron lasers should be able to produce light at wavelengths below 100 nanometers [10]; an optimistic estimate of future technology might make lasers at 10 nm wavelengths possible. Such short wavelengths could not be efficiently produced by direct solar pumped lasers. A more critical limitation on wavelength is the fact that most materials become absorbing below some cut-on wavelength in the UV. Of the dielectric sail materials discussed in the materials section below, silicon carbide films absorb below about 410 nanometers; diamond films below about 250 nanometers. (Actual films absorb some at longer wavelength as well, due to impurities and structural imperfection.) UV windows are conventionally made from fused silica; the best fused silica films start to absorb at about 180 nm. About the best performance can be achieved by halide crystals such as lithium fluoride and calcium fluoride, which begin to absorb at about 130 nm [11]. This represents an improvement of nearly a factor of eight over the baseline 1000 nm laser, and probably represents about the shortest achievable with existing materials.
Such a UV laser would also require a lens transparent in the ultraviolet. This would be the same dielectric material, except with a thickness equal to the reflectance minimum at t =
l/2, rather than the reflectance maximum at t= l/4. It is interesting to note that the mass per unit area will be exactly the same for lens and sail, since the lens is exactly half empty space.An alternate possiblility is that the beam could be electronically steered to correct positioning errors in real time by optical means, rather then by physically moving the lens. An electro-optic element, for example, between the lens and the laser, might be able to correct in real time the lens position error. Alternatively the lens itself could incorporate electro-optic material. Several concepts for such a steering system are possible. Note that the actual amount of steering needed is very small--picoradians--but the amount of energy to be controlled is very high.
The Lens as a Telescope
As a note in passing, the 1000 km lens proposed by Forward, with the pointing accuracy he requires, would make an extremely high magnification telescope [12]. Clearly, a lens focusing to a spot of 100 km at a distance of 4 ly would allow not only planets of nearby stars to be detected, but they could be mapped with a resolution of 100 km. This was the original intention of O'Meara in proposing the paralens. The diffraction-limited beam spread of a 100 km lens for visible light (say 500 nanometer wavelength) would be 0.5 nanoradians. With this resolution, it should be possible to detect Earth-sized planets at a distance of thousands of light years, and Jupiter-sized planets virtually anywhere in the galaxy.
While the paralens will only focus exactly at a single wavelength, it will be approximately focused over a wavelength range of roughly
l/10. Approximating the lens material as a material with constant index of refraction, light with shorter wavelength than the design point will focus farther from the lens than the design focal length, and light with longer wavelength will focus closer to the lens. This will result in chromatic abberation of the image. This abberation is precisely opposite to the chromatic abberation of a normal refractive lens, and could be corrected with an appropriately designed secondary optic. There will also be a wavelength dependent spherical abberation.Star-Sailing With Intermediate Lenses
The lens size required for focusing at interstellar distances is so large that it is productive to search for alternative methods to decrease the lens size needed. An alternative concept is to make the distance small. This is shown in fig. 3. Rather than one large lens, many small lenses are used. Use of a series of lenses has been briefly discussed by Forward [13] for laser-electric propulsion in the solar system. Since the allowed angular divergence due to diffraction is increased by a factor of N, the required lens radius is proportional to the distance between lenses. Each individual lens must be 1/N times the diameter of the single large lens. Since lens area is proportional to the radius squared, if N smaller lenses are used instead of one large lens, the amount of lens material needed is reduced by a factor of N. Clearly, it is to our advantage to make N as large as possible.
Each lens must be pointed and positioned to a high degree of accuracy. For this purpose the lenses would need an intelligent controller, and some sort of reflective steering vanes which could be deployed into the beam as vernier positioners.
The inter-lens spacing d and the lens radius r is chosen such that the difraction-limited beam spread at a single lens spacing is less than or equal to the radius of the lens. Thus, the next lens in the series collects nearly all of the light from the previous lens. In order not to lose too much light in the exponential "tails" of the diffraction, it will be necessary to make each lens somewhat larger than the diffraction-limited minimum. Even a small loss from each lens will reduce the total transmission over the entire lens set significantly.
There will be necessarily some reflection at each lens; this will put a maximum to the optimum number of lenses. If each lens has a reflectance R, the total power reaching the sail will be reduced by (1-R)N. The reflectance per lens must thus be very close to zero. However, half-wave dielectric films can have reflectance values <<1%, so N can in fact be >>100 before reflectance losses become large. Note that radiation darkening of the lens could also reduce transmission; this has not been considered in any detailed analysis to date. Presumably choice of a suitable lens material, such as ceria-doped silica, would minimize this problem.
Deployment of the lenses into position presents a formidable, but solvable, problem. One could imagine the lenses as starting out stacked behind the sail, and deployed as the probe approaches the desired position. If it is desired that the lenses be re-used for subsequent probes, the lenses would have to be stopped once they reach position. Reverse sailing using reflected light from the probe sail could be used to decelerate each lens into position. Re-use of the same lens set for subsequent probes would require that the probe avoid colliding with the lenses as it travels, but since the diameter of the lenses can be as little as 10-10 of the distance between lenses, this presents little difficulty
Alternatively, the lenses could be simply sailed into position by configuring each lens to have a reflectivity designed to give it a chosen acceleration. If the jth lens has an acceleration of j/(N+1) of the probe acceleration, then the lenses will automatically be deployed in equidistant position as the probe accelerates. The laser energy required to accelerate the lenses will equal N2/2 (m
lens/msail) times the energy required to accelerate the sail alone.For the example of a manned mission to epsilon Eridani, one hundred lenses of 10 km diameter, each weighing 56 tons, would be used instead of the proposed single lens of 1000 kilometer diameter weighing 560,000 tons. The total mass of the lenses would be only 5,600 tons, a savings of a factor of a hundred. If each lens has a loss of, for example, 2%, the amount of light remaining at the fiftieth lens (i.e., halfway) is 36% of the initial light. By integrating the amount of light remaining at each lens, it can be calculated that increasing the laser power by increased by a factor of 2 will produce the same average sail acceleration. Depending on whether the lens or the laser is more costly, this could be an effective solution.
Such a concept of many lenses could also be used for other beam-powered interstellar travel methods, such as the "starwisp" proposal [4]. For the proposed high-power, high-speed Epsilon Eridani starwisp probe mission, rather than one 50,000 km diameter lens, which masses 50,000 tons and has a size larger than the diameter of Earth, a hundred 500 km lenses could be used, with a mass of only 5 tons each, for a more reasonable total mass of 500 tons. Such a total mass could be brought to orbit by the space shuttle if a method could be found to deploy such large, flimsy structures from a highly compacted bundle.
As a final comment, discussions of using multiple lenses to focus and refocus the beam inevitably bring up a suggestion that the laser could be dispensed with altogether, and lenses could simply focus solar light collected from, say, near the orbit of Mercury. Unfortunately, this is not possible. The light output from the sun is constant in terms of flux per (heliocentric) solid angle. This is a fundamental optical limitation given by the solid angle of the sun. Use of a lens can change the solid angle, but not the angular flux. Unless the lens diameters approach the solar diameter, there is little advantage over a simple solar sail.
Materials Considerations for a High Power Lightsail
It may be possible to produce higher performance sails than the aluminum sail assumed by Forward. Since the thrust achievable is primarily limited by the maximum allowable sail temperature (due to the sail being heated by the small amount of light absorbed), it may be worthwhile to use a material with a higher melting point than aluminum. If issues of reflectivity and tensile strength at temperature are ignored, the figure of merit for a sail material is T
m/r. For aluminum, the density is 2.7 gr/cm3 and the melting point is 940 K. Other metal have a higher figure of merit, including boron (3.6), beryllium (2.8), scandium (2.1), and titanium (1.5) (figure of merit listed in parenthesis, normalized to Al=1). Boron is extremely strong and lightweight but not highly reflective. Beryllium, with a density of 1.8 and a melt temperature of 1550 K, is apparently the best candidate of the metallic films. The high temperature properties of beryllium sails for solar sail use was noted by Matloff [14].(Note: The original conclusion that beryllium is an ideal sail candidate assumed that the ratio of infrared emissivity to laser absorption is comparable to that of aluminum. Unfortunately, more detailed examination of the optical properties of beryllium indicates that beryllium becomes highly reflective in the infrared, leading to extremely poor emissivity, and hence high sail temperatures. The question of the best sail material should be revisited with more detailed consideration of actual optical properties of materials)
Emissivity is also a major concern in a thermally limited lightsail. It would be useful to increase the emissivity of the front (reflective) side of the sail. At any given wavelength, the emissivity of a film is necessarily equal to the absorptivity, so in general only the back side of the sail can be made highly emissive. However, the sail will be radiating away heat in the infrared, while it is required to be reflective at only a single wavelength, presumably near the visible. It may be possible to make the sail reflective at the wavelength of interest but still emissive in the IR. For example, Flora and Bilger [15] note that a layer of SiO2 can increase emissivity up to 0.91 without significantly deteriorating the optical properties. Although the 25 micron thick film of Flora and Bilger is too heavy for lightsail use, it does suggest the possiblility of finding a coating which is highly emissive in the IR but reflective or transparent to the incident laser light.
Much better performance can be obtained if the sail is a transparent dielectric material rather than a metal film. Alternating layers of high and low index of refraction dielectric films can be made to have high reflectance across a wavelength band [16] (This is also discussed in a later analysis by Forward [17], who suggests an eight-layer composite of quarter-wave diamond films alternating with vacuum). For example, dielectric mirrors, consisting of films of dielectric material on a fused silica base, are commercially available [18] with reflectivity of nearly 99.9% down to a wavelength of 440 nm, and reflectivity of 99.5% down to a wavelength of 325 nm. Most of the light not reflected is transmitted through the film, and very little is absorbed in the dielectric. Damage thresholds for such materials are in the range of 1 MW per square cm. It is also be possible to make such a material with a high emissivity
e at thermal wavelengths on both front and back surfaces. Note that the reflectivity of such layers will drop slightly operated off of design temperature, since thermal expansion will cause the layer thicknesses to move away from optimum.Table 2 shows some dielectric materials and the relevant physical parameters. Although diamond has a melt/sublimation point of over 3500°C, the maximum allowable temperature is set by the diamond to graphite transition temperature of 1800°C [17]. This will allow extremely high thermally-limited acceleration. Using new thin-film diamond technology, extremely thin diamond layers are not difficult to manufacture. Thin layers of diamond are currently produced, for example by glow-discharge decomposition of methane [19]. Tantalum pentoxide and zirconium dioxide are other high refractive index compounds that are used as optical films and are extremely refractory. These can be deposited in thin film form by electron beam evaporation of the compound, or by deposition of the metal followed by oxidation. Zinc sulfide is another compound often used for optical coatings, but is not suitable for high-temperature lightsail use due to the fact that, while the melt temperature is high, ZnS has a high vapor pressure when heated.
However, for a properly designed dielectric film sail, very little of the incident light will be absorbed, and the performance will not be limited by heating of the sail.
Since the probe mass is determined by the sail mass, the optimum dielectric sail is made of a single sheet. Reflectivity is maximum when the thickness of the film is one quarter the wavelength of the light measured inside the film, when the reflected light from the front and rear of the film interfere constructively:
t =
l/(4n) (3)where n is the index of refraction. The higher the refractive index, the fhinner the film can be to provide maximum reflectivity. The reflectivity of a quarter-wave single-layer thin film of a dielectric in vacuum is:
R = [(n2 -1)/(n2 +1)]2 (4)
Additional layers of alternating high and low index material will increase the reflectivity, but less than proportionately to the mass increase.
A single quarter-wavelength diamond film would have a reflectivity of 0.5 and almost negligible absorptance.
The figure of merit of a dielectric film used as a lightsail is the reflectivity (calculated as above) divided by the quarter-wave thickness times the density. This figure, calculated in km2/kg, is equal to the acceleration in gravities possible with a beam intensity of 1.5 kW/m2. The best figure of merit is achieved with the refractory semiconductor silicon carbide, which combines a high index of refraction with a low density. SiC has an absorption edge at about 410 nm (depending on the crystalline phase), which puts a lower limit on the actual laser wavelength allowed. The figure of merit of 60 km2/kg represents an acceleration of 400 gravities per W/cm2, or 0.4 gravities per mW/cm2. Continuous wave power levels of many watts per square centimeter are quite achievable for existing laboratory lasers. Thin SiC layers are currently grown by epitaxial deposition, for example on silicon substrates. For a test sample the silicon could be etched away to leave a free-standing film. The system is apparently eminantly suitable for a small-scale demonstration.
Diamond and silicon have roughly equal figures of merit at about half that of silicon carbide. Silicon has the disadvantage of requiring a much higher laser wavelength, since silicon is strongly absorbing in the visible. It is transparent for wavelengths longer than the Si absorption edge at about 1100 nm, and has low absorptance if it is sufficiently free of dopants, carbon, and oxygen impurities. Silicon is comparatively easy to deposit in thin film form by electron beam evaporation.
Zinc sulfide, zirconium dioxide, and tantalum pentoxide have progressively lower figures of merit. The possible accelerations achievable with any of these films are orders of magnitude higher than those achievable with metal films.
Finally, to see what can be done with a ultraviolet laser, a figure of merit is calculated for lithium fluoride used at a wavelength of 130 nm. Despite the low reflectivity, the figure of merit is reasonable because the short wavelength makes the film thickness very low. (It is unclear, however, whether such thin films of LiF could be made self-supporting.)
Deposition of thin films of ZnS, ZrO2, and Ta2O5 are well developed technologies, unlike the emerging technologies of diamond and silicon carbide thin films. ZrO2, and Ta2O5 are extremely easy to deposit and resistant to most wet chemical etches, and thus it would be straightforward to make a demonstration film by evaporating a thin layer onto a polished substrate (e.g., a silicon wafer) and then removing the substrate by etching.
The reflectivity for wide-spectrum light, such as the solar spectrum, is roughly half of the monochromatic reflectance. Because of the high melt temperature, refractory dielectric films would also be good materials for solar sails for use close to the sun. An alternate possibility could be to start very close to the sun for the initial boost13.
Alternate Concepts for Beam-Propelled Interstellar Flight
A fundamental problem with laser-propelled lightsails is the extremely low energy efficiency of 6.7 nt/GW. The energy efficiency may be greatly improved, at the cost of a reduction in specific impulse, by combining the laser sail with a photovoltaic powered electric (ion) engine. Ion engines in principle have no physical limits on the specific impulse, although extremely high specific inpulses require proportionately high energy consumption. Such a laser-powered rocket would have the ability to decelerate at the target star (with some loss of efficiency), and could also greatly decrease the amount of power required from the laser. Fig. 4 shows a schematic for such a rocket, where the solar array is mounted at a position where the sail acts as a mirror to focus light on it. (The drawing shown implies that the sail is light enough that it will propel itself ahead of the engine and payload; if this is not the case, the ion engine would have to be configured to pull the sail, with, for example, many smaller ion engines firing through individual small openings in the sail.) An alternate version would be to form thin-film solar cells [20] directly on the sail. The specific impulse of such a system can be extremely high as long as the mass flow rate of reaction mass is low; but even with extremely low mass flow rates the energy efficiency of the sail can be greatly improved. A discussion of this point is given by Jackson and Whitmire [21].
Another alternative is to use a beam with a wavelength shorter than light. One such solution is to use a particle beam. Diffraction is not a problem. The particles would have to be charged to be accelerated and focused, and then neutralized to avoid beam expansion due to electrostatic repulsion*. The particles could then be re-ionized and reflected by a magnetic sail [8].
*In the discussion of this point at the 40th IAF Congress, it was suggested that since the interstellar medium is a dilute plasma, it may be possible at sufficiently high beam energies to use an unneutralized beam which is prevented from diverging by its self-generated magnetic field.
A difficulty is beam spread due to random thermal velocity. Thermal beam spread decreases proportionately to the square root of the atomic mass. Using mercury (atomic mass 80) as an example, the lateral velocity due to thermal motion is 1.4 T 1/2 m/sec, where T is the temperature in degrees Kelvin. Existing ion accelerators have typical beam temperatures of hundreds to thousands of degrees, but this can in principal be reduced by any of several known techniques. The limit to the minimum temperature that can be theoretically achieved for the beam is the cosmic background temperature of about 3 K; which would lead to a beam spread of 300,000 km at a distance of 4 LY.
This could be reduced if the beam particles condense to larger particles after acceleration. To reduce the beam spread by a factor of 1000, the number of mercury atoms per condensed droplet needs to be at least a million. This is an extremely small droplet (10-16 grams) by macroscopic terms, and it is not unreasonable to believe that such condensation might take place in the beam. As the droplet size increases, this propulsion concept approaches that of momentum transfer by use of pellet streams, considered for interstellar propulsion by Singer [22].
Conclusions
A laser-pushed light sail is an attractive means of propelling an interstellar probe, since high mass ratios are avoided by using a fixed energy source, but significant difficulties are seen with previous proposals for implementing such a propulsion system [3].
The large lens required and high lens/target distance results in optical difficulties in such a system, requiring positioning tolerance for the thousand kilometer lens of only 3 meters, which is unlikely to be achievable. Some advantage can be gained by using a lightsail reflective in a shorter wavelength regime. LiF and CaF2 quarter wave dielectric films are suggested, which are reflective down to around 130 nm, an improvement of almost a factor of eight. Another technique for reducing the problem would be to use many intermediate lenses spaced between the probe and the source. A hundred intermediate lenses, for example, would reduce the individual lens mass by a factor of ten thousand and reduce the total lens mass from the initial 560,000 tons to a more reasonable 5,600 tons. Pointing, positioning, and deployment problems would, however, be great.
Quarter wavelength dielectric films have significant advantages over metals as sail materials. The highest figure of merit was for a silicon carbide film, with a figure of merit of 60 km2/kg, allowing a theoretical acceleration of 0.4 gravities per mW/cm2 laser power. This is amenable to testing on a laboratory scale.
Finally, two other beam-propulsion systems were discussed, the use of a laser energized ion rocket, and the idea of using a particle beam instead of a laser beam.
Acknowledgements
I would like to acknowledge the useful comments, suggestions, discussions, and criticisms of Dr. Robert Forward concerning material discussed in this paper, not all of which was incorporated into the text. I would also like to thank Colin McInnes and Phillip Jenkins for comments.
References
[1] Forward, R.L., "Pluto: Gateway to the Stars," Missiles and Rockets, Vol. 10, April 1962, pp. 26-28.
[2] Marx, G., "Interstellar Vehicle Propelled by Terrestrial Laser Beam," Nature, Vol. 213, July 2 1966, pp. 22-23.
[3] Forward, R.L., "Roundtrip Interstellar Travel Using Laser-Pushed Lightsails," J. Spacecraft and Rockets, Vol. 21, March-April 1984, pp. 187-195.
[4] Forward, R.L., "Starwisp: An Ultra-Light Interstellar Probe", J. Spacecraft and Rockets, Vol. 22, May-June 1985, 345-350.
[5] Jones, E.M., "A Manned Interstellar Vessel Using Microwave Propulsion: A Dysonship," J. Brit. Interplanetary Soc., Vol. 38, June 1985, pp. 270-273.
[6] Forward, R.L., "Zero Thrust Velocity Vector Control for Interstellar Probes," AIAA Journal, May 1964, pp. 885-889.
[7] Norem, P.C., "Interstellar Travel: A Propulsion System with Relativistic Velocity Capability," AAS Paper 69-338, June 1969.
[8] Andrews, D.G., and Zubrin, R.M., "Magnetic Sails and Interstellar Travel," IAF Paper IAF-88-5533, October 1988.
[9] The version of this paper presented at the IAF Congress in 1989 also stated that the diameter of the aperture of the laser must be less than the allowable 6 meter error. I thank Robert Forward (personal communication, 1989) for showing that this is only true for an incoherent light source.
[10] Brau, C.A., "Free Electron Lasers are Ready to Prove Themselves," Laser Focus, Vol. 24, April 1988, pp. 20-26.
[11] Wolfe, W.L., "Properties of Optical Materials," Handbook of Optics, W.G. Driscoll, ed., McGraw-Hill, NY, 1978, p. 7-16, 7-40.
[12] Forward, R.L., Flight of the Dragonfly, Pocket Books, NY, 1984 (in revised form under the title Rocheworld, Baen Books, 1990).
[13] Forward, R.L., Advanced Propulsion Concepts Study, Comparison of SEP and Laser Electric Propulsion, Final Report, JPL Contract 954085, June 1985, Figure 1 and p. 7.
[14] Matloff, G.L., "Interstellar Solar Sailing: Consideration of Real and Projected Sail Materials," J. British Interplanetary Soc., Vol. 37, March 1984, pp. 135-141.
[15] Flora, C. and Bilger, K.M., "Development of a High Emissivity Coating for Silicon Solar Cells," Space Photovoltaic Research and Technology Conference 1988, NASA Lewis Research Center, 1988.
[16 Chopra, K.L., "Optical Properties of Thin Films," Chapter XI of Thin Film Technology, McGraw Hill, 1969.
[17] Forward, R.L., "Laser Weapon Target Practice with Gee-whiz Targets," presented at Laser Propulsion Workshop, Lawrence Livermore National Laboratories, 7-18 July 1986.
[18] Newport Catalog 1989, Chapter N: Optics, p. N-76-77 and N-104. Newport Corporation, P.O. Box 8020, Fountain Valley, CA 92728.
[19] Kobayashi, K., Mutsukura, N., and Machi, Y., "Deposition of Hard Carbon Films by RF Glow Discharge Method," J. Appl. Phys., Vol. 59, 1 February 1986, pp. 910-912.
[20] Landis, G.A., Flood, D.J., and Bailey, S.J., "Advances in Thin-Film Solar Cells for Light Weight Space Photovoltaic Power" NASA TM-102017, Space Power, Vol. 8 No. 1/2, 1989, pp. 31-50.
[21] Jackson, A.A., and Whitmire, D.O, "Laser Powered Interstellar Rocket," J. British Interplanetary Soc., Vol. 31, Sept. 1978, pp. 335-337.
[22] Singer, C.E., "Interstellar Propulsion Using a Pellet Stream for Momentum Transfer," J. British Interplanetary Soc., Vol. 33, Mar. 1980, pp. 107-115.
Table 1:
Summary of parameters of three interstellar lightsail missions proposed by Forward.
Laser Vehicle Sail
Stage Power Mass Accel. diam. Velocity
1. Flyby Mission
outbound 65 GW 1 ton 0.036 g 3.6 km 0.11c@ 0.17 ly
2. Rendezvous Mission
outbound 7,200 GW 785 tons 0.3 g 100 km 0.21c@2.1 ly
decel. 26,000 GW 71 tons 0.2 g 30 km 0 @ 4.3 ly
3. Manned Mission
outbound 75,000,000 GW 78,500 tons 0.3 g 1000 km 0.5c @ 0.4 ly
decel. 17,000,000 GW 7,850 tons 0.3 g 320 km 0 @10.4 ly
return 17,000,000 GW 785 tons 0.3 g 100 km 0.5c@ 10.4 ly
decel. 430,000 GW 785 tons 0.3 g 100 km 0@ 0.4 ly
Table 2:
Physical Properties of Refractory Dielectric Materials
Material Max Temp Density
( C ) (gr/cm3)
Diamond 1800* 3.5 (*graphite conversion[16])
Silicon 1410 2.4 (absorbs below 1200 nm)
Silicon Carbide 2000* 3.17 (*sublimes)
Zinc sulfide 450* 3.9 (*sublimes)
Tantalum Pentoxide 1870 8.75
Zirconium dioxide 2715 5.5
Silicon dioxide 1600 2.7
Lithium fluoride 820 2.6
Table 3:
Dielectric Films: Figure of Merit for Use as Solar Sail
figure of merit R/T
r equals reflectivity/(thickness.density)
(gr/cm3) (nm) (kg/km2) (%) (km2/kg)
Visible
Diamond 3.51 2.41 42 147 50 34
SiC 3.17 2.65 29 92 56 61
ZnS 3.9 2.35 43 166 48 29
Ta2O5 8.75 2.5 40 350 52 15
ZrO2 5.49 2.15 47 260 42 16
Infrared
Si 2.4 3.5* 85.* 205* 72* 35.*
*at wavelength of 1200 nm
Ultraviolet
LiF 2.60 1.45 22.* 58* 12* 21.*
*at wavelength of 130 nm
Figures

1. Schematic of the round-trip interstellar lightsail concept proposed by Forward (not to scale), shown during the deceleration phase.
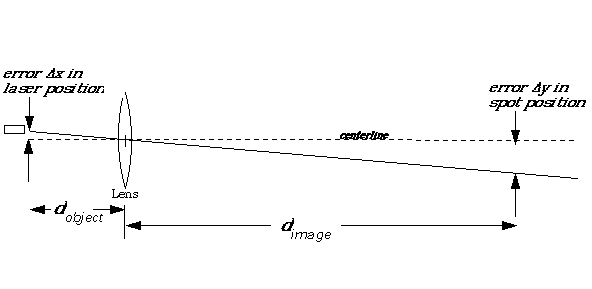
2. Optical magnification of the lens/laser system.
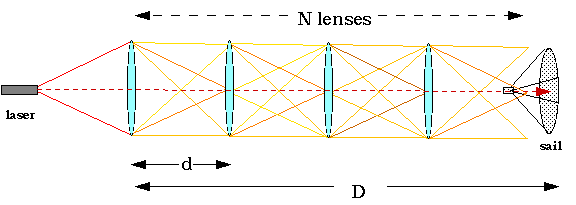
3. Use of multiple intermediate lenses to propel a lightsail.
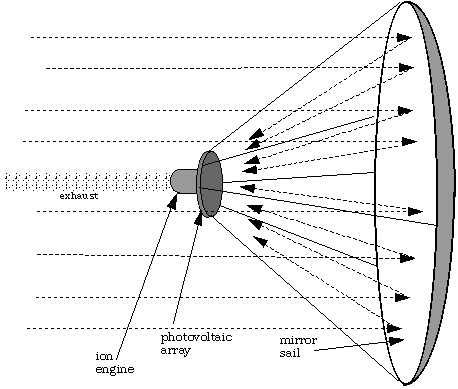
4. Use of a sail as an energy source for an ion engine.